|
|
Home ► Placements ► Interview Questions ► Aptitude Interview Questions And Answers Page18 ▼
| Aptitude Interview Questions And Answers |
|
79. When processing flower-nectar into honeybees' extract, a considerable amount of water gets reduced. How much flower-nectar must be processed to yield 1kg of honey, if nectar contains 50% water, and the honey obtained from this nectar contains 15% water?
Solution:
Flower-nectar contains 50% of non-water part.
In honey this non-water part constitutes 85% (100-15).
Therefore 0.5 X Amount of flower-nectar = 0.85 X Amount of honey = 0.85 X 1 kg
Therefore amount of flower-nectar needed = (0.85/0.5) * 1kg = 1.7 kg. |
|
80. Two boys begin together to write out a booklet containing 535 lines. The first boy starts with the first line, writing at the rate of 100 lines an hour; and the second starts with the last line then writes line 534 and so on, backward proceeding at the rate of 50 lines an hour. At what line will they meet?
Solution:
Writing ratio = 100:50= 2:1
Since equal quantities are taken,
Therefore in a given time, first boy will be writing the line number
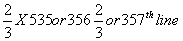 <> <>
Hence, both of them shall meet on 357th line
|
|
81. If the price of petrol increases by 25%, by how much must a user cut down his consumption so that his expenditure on petrol remains constant?
Solution:
Let the price of petrol be Rs.100 per litre. Let the user use 1 litre of petrol. Therefore, his expense on petrol = 100 * 1 = Rs.100
Now, the price of petrol increases by 25%. Therefore, the new price of petrol = Rs.125.
As he has to maintain his expenditure on petrol constant, he will be spending only Rs.100 on petrol.
Let ‘x’ be the number of litres of petrol he will use at the new price.
Therefore, 125*x = 100 => x = 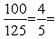 0.8 litres. 0.8 litres.
He has cut down his petrol consumption by 0.2 litres = 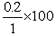 = 20% reduction. = 20% reduction.
There is a short cut for solving this problem.
If the price of petrol has increased by 25%, it has gone up 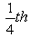 of its earlier price. of its earlier price.
Therefore, the % of reduction in petrol that will maintain the amount of money spent on petrol constant = 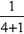 = = 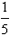 = 20% = 20%
|
|
82. A train traveling at 72 kmph crosses a platform in 30 seconds and a man standing on the platform in 18 seconds. What is the length of the platform in meters?
Solution:
When the train crosses a man standing on a platform, the distance covered by the train is equal to the length of the train.
However, when the same train crosses a platform, the distance covered by the train is equal to the length of the train plus the length of the platform.
The extra time that the train takes when crossing the platform is on account of the extra distance that it has to cover = length of the platform.
Therefore, length of the platform = speed of train * extra time taken to cross the platform
Length of platform = 72 kmph * 12 seconds
converting 72 kmph into m/sec, we get 72 kmph = 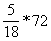 = 20 m/sec = 20 m/sec
Therefore, length of the platform = 20 * 12 = 240 meters.
|
|

|
