|
73. A candidate who gets 20% marks fails by 10 marks but another candidate who gets 42% marks gets 12% more than the passing marks. Find the maximum marks.
Solution:
Let the maximum marks be x.
From the given statement pass percentage is 42% - 12% = 30%
By hypothesis, 30% of x – 20% of x = 10 (marks)
i.e., 10% of x = 10
Therefore, x = 100 marks |
|
74. Train A traveling at 60 km/hr leaves Mumbai for Delhi at 6 P.M. Train B traveling at 90 km/hr also leaves Mumbai for Delhi at 9 P.M. Train C leaves Delhi for Mumbai at 9 P.M. If all three trains meet at the same time between Mumbai and Delhi, what is the speed of Train C if the distance between Delhi and Mumbai is 1260 kms?
Solution:
All three trains meet at the same time between Delhi and Mumbai. Which means Train A and Train B are at the same point at that time. This will happen when Train B is overtaking Train A.
Train A starts 3 hours before Train B. Therefore, by the time Train B leaves Mumbai, Train A has covered 3 * 60 = 180 kms.
The relative speed between Train A and Train B = 90 - 60 = 30 kmph. Therefore, Train B will overtake Train A in 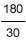 = 6 hours from the time Train B leaves Mumbai. That is at 3 A.M, Train B will overtake Train A. The point between Mumbai and Delhi at which Train B overtakes Train A will be 6*90=540 kms from Mumbai. = 6 hours from the time Train B leaves Mumbai. That is at 3 A.M, Train B will overtake Train A. The point between Mumbai and Delhi at which Train B overtakes Train A will be 6*90=540 kms from Mumbai.
Train C will also be at that point at 3 A.M while Train B is overtaking Train A. And Train C would have travelled 1260-540 = 720 kms in these 6 hours. Therefore, the speed of Train C =  = 120 km/hr. = 120 km/hr.
|
|
75. In an election contested by two parties, Party D secured 12% of the total votes more than Party R. If party R got 132,000 votes, by how many votes did it lose the election?
Solution:
Let the percentage of the total votes secured by Party D be x%
Then the percentage of total votes secured by Party R = (x – 12)%
As there are only two parties contesting in the election, the sum total of the votes secured by the two parties should total up to 100%
i.e., x + x – 12 = 100
2x – 12 = 100
or 2x = 112 or x = 56%.
If Party D got 56% of the votes, then Party got (56 – 12) = 44% of the total votes.
44% of the total votes = 132,000 i.e., 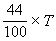 = 132,000 = 132,000
ð T = 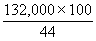 = 300,000 votes. = 300,000 votes.
The margin by which Party R lost the election = 12% of the total votes
= 12% of 300,000 = 36,000.
|
