|
61.
A and B enter in to a partnership and A invests Rs. 10,000 in the partnership. At the end of 4 months he withdraws Rs.2000. At the end of another 5 months, he withdraws another Rs.3000. If B receives Rs.9600 as his share of the total profit of Rs.19,100 for the year, how much did B invest in the company?
Sol:
The total profit for the year is 19100. Of this B gets Rs.9600. Therefore, A would (19100 – 9600) = Rs.9500.
The partners split their profits in the ratio of their investments.
Therefore, the ratio of the investments of A : B = 9500 : 9600 = 95 : 96.
A invested Rs.10000 initially for a period of 4 months. Then, he withdrew Rs.2000.
Hence, his investment has reduced to Rs.8000 (for the next 5 months).
Then he withdraws another Rs.3000. Hence, his investment will stand reduced to Rs.5000
during the last three months.
So, the amount of money that he had invested in the company on a money-month basis
will be = 4 * 10000 + 5 * 8000 + 3 * 5000 = 40000 + 40000 + 15000 = 95000
If A had 95000 money months invested in the company, B would have had 96,000
money months invested in the company (as the ratio of their investments is 95 : 96).
If B had 96,000 money-months invested in the company, he has essentially invested 96000/12 = Rs.8000.
|
|
62.
Four horses are tethered at 4 corners of a square field of side 70 metres so that they just cannot reach one another. The area left ungrazed by the horses is:
Sol:
The length of the rope in which the horses tied should be equal to half of the side of the
square plot so that they just cannot reach one another.
Therefore, the length of the rope is 35m (70/2).
The area covered by each horse should be equal to the area of sector with radius of 70/2 =
35m(length of the rope).
Total area covered by the four horses = 4* area of sector of radius 35 metres = Area of
circle of radius 35m.
Area left ungrazed by the horses = Area of square field - Area covered by four horses.
= 702 - (22/7)*35*35 = 4900 - 3850 = 1050 sq.m. |
|
63.
The area of a square field is 24200 sq m. How long will a lady take to cross the field diagonally at the rate of 6.6 km/hr?
Sol: Let ‘a’ meters be the length of a side of the square field.
Therefore, its area = a2 square meters. --- (1)
We know that the length of the diagonal ‘d’ of a square whose side is ‘a’ meters =
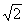 a –-- (2) a –-- (2)
From (1) and (2), we can deduce that the square of the diagonal = d2 = 2a2
Or d = 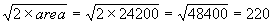 meters. meters.
The time taken to cross a length of 220 meters while traveling at 6.6 kmph is
given by 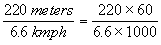 (converting (converting
1 km = 1000 meters and 1 hour = 60 minutes).
= 2 minutes
|
|
64.
For what values of 'm' is y = 0, if y = x2 + (2m + 1)x + m2 - 1? x is a real number.
(1) m 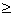 -2 -2
(2) m < 0
(3) m = 0
(4) m  -1.25 -1.25
Sol:
When x is real, then the discriminant of a quadratic equation (ax2 + bx + c = 0) 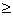 0. 0.
i.e. D = b2 - 4ac  0 0
In this case,
(2m + 1)2 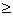 4(m2 - 1) 4(m2 - 1)
4m2 + 4m + 1 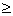 4(m2 - 1) 4(m2 - 1)
Solving for m, we get m 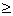 - 1.25 - 1.25
|
