|
Description:
This program is the example of encryption and decryption.For the encryption and decryption any algorithm must be implemented. RSA can be used to encrypt or decrypt a String. It is a public key algorithm (i.e. two different keys are used to encrypt and decrypt the data). However these two keys are related. RSA involves a public key and a private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted using the private key. BigIntegers are necessary for implementing RSA algorithm. The java.math.BigInteger class is used for representing immutable arbitrary-precision integers. BigInteger provides analogues to all of Java's primitive integer operators, and all relevant methods from java.lang.Math.
Encryption and Decryption of a password using RSA Using Java:
/*PwdEncryption.java*/
import java.math.*;
public class PwdEncryption{
public static void main(String args[]){
String nhash;
BigInteger[] ciphertext = null;
BigInteger n = null;
BigInteger d = null;
String password="Java";
System.out.println("Password (Input) : "+ password);
RSA rsa = new RSA( 8 ) ;
n=rsa.getN();
d=rsa.getD();
ciphertext = rsa.encrypt(password) ;
StringBuffer bf = new StringBuffer();
for( int i = 0 ; i < ciphertext.length ; i++ )
{
bf.append( ciphertext[i].toString( 16 ).toUpperCase() ) ;
if( i != ciphertext.length - 1 )
System.out.print( " " ) ;
}
String message=bf.toString();
System.out.println();
System.out.println("Encrypted Message : "+message);
String dhash = rsa.decrypt( ciphertext ,d,n) ;
System.out.println();
System.out.println("Decrypted Message : "+dhash);
}
}
/* RSA.java*/
import java.math.BigInteger ;
import java.util.Random ;
import java.io.* ;
public class RSA
{
/**
* Bit length of each prime number.
*/
int primeSize ;
/**
* Two distinct large prime numbers p and q.
*/
BigInteger p, q ;
/**
* Modulus N.
*/
BigInteger N ;
/**
* r = ( p - 1 ) * ( q - 1 )
*/
BigInteger r ;
/**
* Public exponent E and Private exponent D
*/
BigInteger E, D ;
public RSA(){
}
/**
* Constructor.
*
* @param primeSize Bit length of each prime number.
*/
public RSA( int primeSize )
{
this.primeSize = primeSize ;
// Generate two distinct large prime numbers p and q.
generatePrimeNumbers() ;
// Generate Public and Private Keys.
generatePublicPrivateKeys() ;
}
/**
* Generate two distinct large prime numbers p and q.
*/
public void generatePrimeNumbers()
{
p = new BigInteger( primeSize, 10, new Random()) ;
do
{
q = new BigInteger( primeSize, 10, new Random()) ;
}
while( q.compareTo( p ) == 0 ) ;
}
/**
* Generate Public and Private Keys.
*/
public void generatePublicPrivateKeys()
{
// N = p * q
N = p.multiply( q ) ;
// r = ( p - 1 ) * ( q - 1 )
r = p.subtract( BigInteger.valueOf( 1 ) ) ;
r = r.multiply( q.subtract( BigInteger.valueOf( 1 ) ) ) ;
// Choose E, coprime to and less than r
do
{
E = new BigInteger( 2 * primeSize, new Random() ) ;
}
while( ( E.compareTo( r ) != -1 ) || ( E.gcd( r ).compareTo( BigInteger.valueOf( 1 ) ) != 0 ) ) ;
// Compute D, the inverse of E mod r
D = E.modInverse( r ) ;
}
/**
* Encrypts the plaintext (Using Public Key).
*
* @param message String containing the plaintext message to be encrypted.
* @return The ciphertext as a BigInteger array.
*/
public BigInteger[] encrypt( String message )
{
int i ;
byte[] temp = new byte[1] ;
byte[] digits = message.getBytes() ;
BigInteger[] bigdigits = new BigInteger[digits.length] ;
for( i = 0 ; i < bigdigits.length ; i++ )
{
temp[0] = digits[i] ;
bigdigits[i] = new BigInteger( temp ) ;
}
BigInteger[] encrypted = new BigInteger[bigdigits.length] ;
for( i = 0 ; i < bigdigits.length ; i++ )
encrypted[i] = bigdigits[i].modPow( E, N ) ;
return( encrypted ) ;
}
public BigInteger[] encrypt( String message,BigInteger userD,BigInteger userN)
{
int i ;
byte[] temp = new byte[1] ;
byte[] digits = message.getBytes() ;
BigInteger[] bigdigits = new BigInteger[digits.length] ;
for( i = 0 ; i < bigdigits.length ; i++ )
{
temp[0] = digits[i] ;
bigdigits[i] = new BigInteger( temp ) ;
}
BigInteger[] encrypted = new BigInteger[bigdigits.length] ;
for( i = 0 ; i < bigdigits.length ; i++ )
encrypted[i] = bigdigits[i].modPow( userD, userN ) ;
return( encrypted ) ;
}
/**
* Decrypts the ciphertext (Using Private Key).
*
* @param encrypted BigInteger array containing the ciphertext to be decrypted.
* @return The decrypted plaintext.
*/
public String decrypt( BigInteger[] encrypted,BigInteger D,BigInteger N )
{
int i ;
BigInteger[] decrypted = new BigInteger[encrypted.length] ;
for( i = 0 ; i < decrypted.length ; i++ )
decrypted[i] = encrypted[i].modPow( D, N ) ;
char[] charArray = new char[decrypted.length] ;
for( i = 0 ; i < charArray.length ; i++ )
charArray[i] = (char) ( decrypted[i].intValue() ) ;
return( new String( charArray ) ) ;
}
/**
* Get prime number p.
*
* @return Prime number p.
*/
public BigInteger getp()
{
return( p ) ;
}
/**
* Get prime number q.
*
* @return Prime number q.
*/
public BigInteger getq()
{
return( q ) ;
}
/**
* Get r.
*
* @return r.
*/
public BigInteger getr()
{
return( r ) ;
}
/**
* Get modulus N.
*
* @return Modulus N.
*/
public BigInteger getN()
{
return( N ) ;
}
/**
* Get Public exponent E.
*
* @return Public exponent E.
*/
public BigInteger getE()
{
return( E ) ;
}
/**
* Get Private exponent D.
*
* @return Private exponent D.
*/
public BigInteger getD()
{
return( D ) ;
}
/**
* RSA Main program for Unit Testing.
*/
public static void main( String[] args ) throws IOException
{
/*if( args.length != 1 )
{
System.out.println( "Syntax: java RSA PrimeSize" ) ;
System.out.println( "e.g. java RSA 8" ) ;
System.out.println( "e.g. java RSA 512" ) ;
System.exit( -1 ) ;
}
// Get bit length of each prime number
int primeSize = Integer.parseInt( args[0] ) ;*/
int primeSize =8;
// Generate Public and Private Keys
RSA rsa = new RSA( primeSize ) ;
System.out.println( "Key Size: [" + primeSize + "]" );
System.out.println( "" ) ;
System.out.println( "Generated prime numbers p and q" );
System.out.println( "p: [" + rsa.getp().toString( 16 ).toUpperCase() + "]" );
System.out.println( "q: [" + rsa.getq().toString( 16 ).toUpperCase() + "]" );
System.out.println( "" ) ;
System.out.println( "The public key is the pair (N, E) which will be published." ) ;
System.out.println( "N: [" + rsa.getN().toString( 16 ).toUpperCase() + "]" ) ;
System.out.println( "E: [" + rsa.getE().toString( 16 ).toUpperCase() + "]" ) ;
System.out.println( "" ) ;
System.out.println( "The private key is the pair (N, D) which will be kept private." ) ;
System.out.println( "N: [" + rsa.getN().toString( 16 ).toUpperCase() + "]" ) ;
System.out.println( "D: [" + rsa.getD().toString( 16 ).toUpperCase() + "]" ) ;
System.out.println( "" ) ;
// Get message (plaintext) from user
System.out.println( "Please enter message (plaintext):" ) ;
String plaintext = ( new BufferedReader( new InputStreamReader( System.in ) ) ).readLine() ;
System.out.println( "" ) ;
// Encrypt Message
BigInteger[] ciphertext = rsa.encrypt( plaintext ) ;
System.out.print( "Ciphertext: [" ) ;
for( int i = 0 ; i < ciphertext.length ; i++ )
{
System.out.print( ciphertext[i].toString( 16 ).toUpperCase() ) ;
if( i != ciphertext.length - 1 )
System.out.print( " " ) ;
}
System.out.println( "]" ) ;
System.out.println( "" ) ;
RSA rsa1 = new RSA(8);
String recoveredPlaintext = rsa1.decrypt( ciphertext ,rsa.getD(),rsa.getN()) ;
System.out.println( "Recovered plaintext: [" + recoveredPlaintext + "]" ) ;
}
}
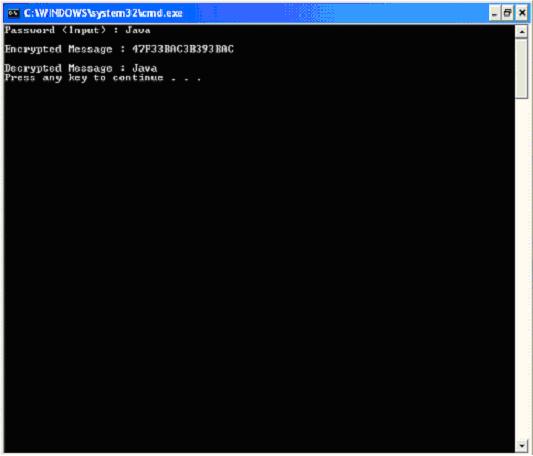
Sample ScreenShot:
|

